大人になると小学校で習ったことなんて大分忘れていますよね。
小学校で習う理科も、きちんと覚えておくと色々と役に立ちますので覚えておきましょう。
てこの原理 作用点、支点、力点、の順番の場合
一言でてこの原理と言っても、支点の位置によって力のかかり具合や方向が変わってきます。
ここでは作用点、支点、力点、の順番の場合について書いていきます。
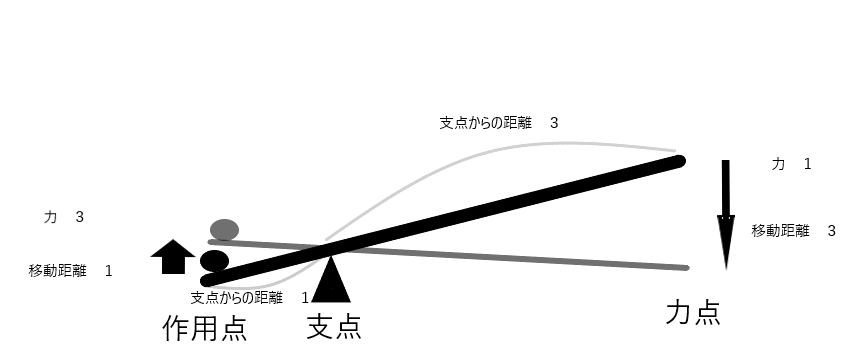
上の図に概略を書きましたが、例として
作用点と支点間の距離 対 支点と力点間の距離が 1:3の場合
- 1の力で3の重さのものを持ち上げる事が出来る
- 1の距離重りを動かすためには、3の距離移動させなければならない
- 力点に加えた力と作用点に加わった力は向きが逆になる
この内容を覚えておけば大丈夫です。
力と距離の関係は
作用点での力の大きさ×支点から作用点までの距離=力点の力の大きさ×支点から力点までの距離
つまり、重いものを出来るだけ小さな力で動かしたいときは
動かいたいものと支点を出来るだけ近くし、力を加える場所は支点から出来るだけ遠くすれば良いという事です。(但し、動かしたいものは少ししか動きません)
てこの原理も、正確に数値で出すためには力のベクトルがどうとか、棒の強度(たわみ)がどうとかの話になりますが、これは物理学の範疇になりかなり面倒くさい話になりますので、ここでは細かいところは無視しています。
別の記事で書きますが、はさみを使う時にてこの原理を覚えておくとはさみの能力を効率よく使う事が出来ます。
てこの原理 支点、作用点、力点、の順番の場合
前記の説明と同じ 長さ4の棒を使って 支店、作用点、力点、の順番の場合は
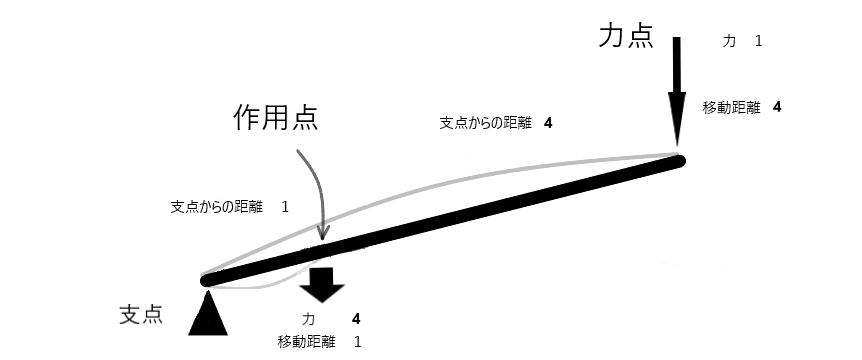
支点と作用点間の距離 対 支点と力点間の距離が 1:4の場合
- 1の力を使うことで4の力で押し付けることが出来る
- 1の距離重りを動かすためには、4の距離移動させなければならない
- 力点に加えた力と作用点に加わった力は同じ向きになる
こちらの場合も
作用点での力の大きさ×支点から作用点までの距離=力点の力の大きさ×支点から力点までの距離
という法則は同じです。
くるみ割り器や蓋のオープナーはこの原理が使われています
小さい力でも 大きな力で掴んだり、押し付けることが出来ます。
Amazonプライム無料体験で送料無料・お届け日指定。
他にも、DIYや何かの作業で力仕事をするときも無駄に疲れず力を効率よく使う事が出来ますので、力仕事をするときにはてこの原理を思い出してみましょう。
何か曲げたいものがあって力がうまく掛からず曲げられないときは、
・曲げたい箇所を支点にして
・片方(できれば短い方)を固定し
・もう一方を何かで延長させて力を加える と
小さな力でも曲げる事が出来ます。
てこの原理を応用したものの代表として鋏の使い方もどうぞ


























コメント